Question

Find an equation of the tangent line at each of the four (4) of points on the curve (x 2 +y 2 −4x) 2 = 2(x 2 +y 2 ) where x = 1. This curve, whose general equation is given by (x 2 + y 2 − ax) 2 = b 2 (x 2 + y 2 ), for constants a and b, is an example of a lima¸con of Pascal, named after French philosopher Blaise Pascal’s father, Etienne ´ Pascal, who first described it in 1650.

Answer 1

`y=\pm(1)/(3)(x-1)\pm 1\\\\y=\pm(5√(7))/(21)(x-1)\pm√(7)`

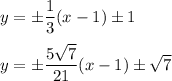
Explanation:

To write an equation of the tangent lines, we need to know the locations of the tangent points, and the slope of the curve at those locations. To find the slope of the curve, we can implicitly differentiate and solve for dy/dx at x=1.

The derivative with respect to x of the given equation is ...

`2(x^2+y^2-4x)(2x+2yy'-4)=2(2x+2yy')\\\\(y^2-3)(yy'-1)=1+yy' \qquad\text{divide by 4 and substitute $x=1$}\\\\y'=(y^2-2)/(y(y^2-4))`

__

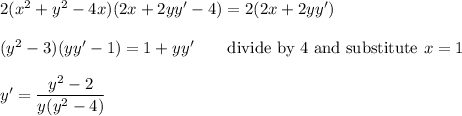
The points of tangency are the solutions to the given equation when x=1. Substituting z=y^2, that equation becomes ...

`(1+z-4)^2=2(1+z)\\\\z^2-8z+7=0 \qquad\text{subtract the right side}\\\\(z-7)(z-1)=0 \qquad\text{factor}`

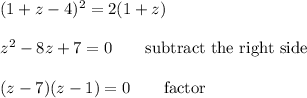
Solutions are z=7 or z=1, so ...

`y=\pm 1\\y=\pm√(7)`

__

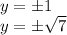
Putting these point values into the equation for the slope, we find ...

`y'=(1-2)/((\pm 1)(1-4))=\pm(1)/(3)\\\\y'=(7-2)/((\pm√(7))(7-4))=\pm(5√(7))/(21)`

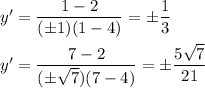
Then the tangent lines have equations ...

`y=\pm(5√(7))/(21)(x-1)\pm√(7)\\\\y=\pm(1)/(3)(x-1)\pm 1`

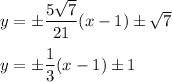
These are shown in the attached graph.