Question

when 9 is subtracted from the square of a number, the result is 8 times the number.Find the negative soulution.PLZ HELP FAST

Answer 1

The negative solution k = -1 is the desired solution.

Explanation:

Let the given number = k

So, according to the question:

`k^(2)  - 9 = 8k`

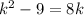
or,
`k^(2)  - 8k - 9 = 0`

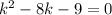
Now, solving this quadratic equation, we get

`\implies k^(2)  - 9k + k - 9 = 0`

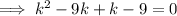
or, k ( k-9) + 1 (k-9) = 0

⇒( k-9)(k+1) = 0

or, ( k-9) = 0 , or (k+1) = 0

⇒ k = 9 or k = -1

Since we only want the negative solution , the k = -1 is the desired solution.