Volume of cylinder is 3 times of volume of cone having same base diameter and same height.
Solution:
Given that
A cylinder and A cone have the same diameter = 10 inches and same height = 12 inches
Need to find the relationship between volume of cylinder and cone.
Let’s calculate volume of each object separately first.
Calculation of volume of cylinder :
Formula of volume of cylinder is given as:
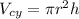
Where π=3.14
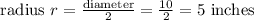
height h = 12 inches
On substituting given values in formula of cylinder we get

Calculation of volume of cone:
Formula of volume of cone is given as:
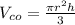
Here π=3.14
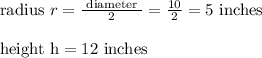
On substituting given values in formula of cone we get
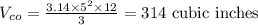
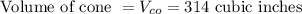
On comparing the two volumes we get
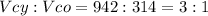
Hence can conclude that Volume of cylinder is 3 times of volume of cone having same base diameter and same height.