Question

A triangular lot is 150 ft on one side and has a property line of length 900 ft. Find the area of the lot in acres.​

Answer 1

The area of the lot is 1.514 acres.

First we need to find the height of the lot.

We can do this by using the Pythagorean theorem because we can think of the lot as a right triangle with a 900-foot hypotenuse and a leg length of 150 feet.

The other leg (the height of the lot) would then have length \begin{align*}

`√(900^2 - 150^2) &= √(810000 - 22500) \&= √(787500) \&= 887.5.\end{align*}`

Thus the area of the lot is
`(1)/(2)` bh=
`(1)/(2)` ⋅150⋅887.5= 66062.5 ​square feet.

Since 1 acre is 43560 square feet, the area of the lot is 66062.5/43560= 1.514 acres.

Answer 2

Answer: Area of plot is 1.549 acres.

Explanation:

Since we have given that

Length of base of triangular plot = 150 ft

Length of property line = 900 ft

We need to find the area of plot in acres.

As we know the formula for "Area of triangle":

Area of triangle is given by

`(1)/(2)* 150* 900\\\\=67500\ ft^2`

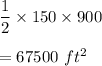
Area in acres would be

`(67500)/(43560)\\\\=1.549\ acres`

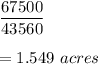
Hence, area of plot is 1.549 acres.