Question

After deciding to buy a new car, you can either lease the car or purchase it on a two-year loan. The car you wish to buy costs $38,500. The dealer has a special leasing arrangement where you pay $106 today and $506 per month for the next two years. If you purchase the car, you will pay it off in monthly payments over the next two years at an APR of 7 percent. You believe you will be able to sell the car for $26,500 in two years. What break-even resale price in two years would make you indifferent between buying and leasing? (Do not round intermediate calculations and round your final answer to 2 decimal places, e.g., 32.16.)

Answer 1

net present value = 15452.63

present value of future monthly payment = 11301.56

resale price= 31151.05

Step-by-step explanation:

given data

buy costs = $38,500

monthly rate = 7 % =
`(0.07)/(12)`

no of period = 2 × 12 = 24

solution

we find present value of resale is

present value =
`(26500)/((1+((0.07)/(12)))^(24))`

present value = 23047.37

so

net present value of purchase car is = purchase cost - present value

net present value = 38500 - 23047.37 = 15452.63

and

present value of future monthly payment is

present value of future monthly payment = 506 ×
`((1-(1+((0.07)/(12)))^(-24))/((0.07)/(12))`

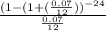
present value of future monthly payment = 11301.56

so present value of leasing car = today payment + present value of future monthly payment

resent value of leasing car = 106 + 11301.56

resent value of leasing car = 11407.56

we consider resale price = x

so break even sale price = 38500 -
`(x)/((1+((0.07)/(12))^(24))`

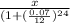
solve we get

x = 31151.05

so resale price= 31151.05