–3x + 3y - 4 =0 and - x + y -3 = 0 do not have any solution which means two lines are parallel and there will be no intersection point.
Solution:
Need to determine solution of following system of equations
–3x + 3y = 4
y = x + 3
Let's modify given equation in standard form
–3x + 3y - 4 =0 ------- (1)
- x + y -3 = 0 ------- (2)
Lets first analyze whether given system of equation is having solution or not.
If
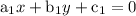 and
and
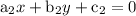 are two equation, then if,
are two equation, then if,
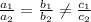 then the given system of equation has no solution.
then the given system of equation has no solution.
In this problem,
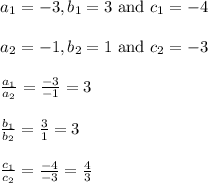
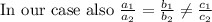
So equations –3x + 3y - 4 =0 and - x + y -3 = 0 do not have any solution which means two lines are parallel and there will be no intersection point.