The following system of equations 8x - 12y = -9 and 18x + 27y = 21 are intersecting lines
Solution:
Given, system of equations are 8x – 12y = - 9 ⇒ (1)
And 18x + 27y = 21 ⇒ 6x + 9y = 7 ⇒ (2)
We have to classify the above given system of equations
For the we have to find the solution for the given system of equations
So, now, multiply (1) with 9 and (2) with 12, such that both equations will have same coefficients for y terms, such that, it will be easier to find solution while calculations by cancelling.
72x – 108y = - 81
72x + 108y = 84
(+) ---------------------------
144x + 0y = 3
144x = 3

Substitute "x" value in (2)
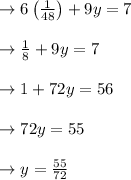
So, given system of equations has 1 solution
 which means that, they are intersecting lines.
which means that, they are intersecting lines.
Hence, the given system of equations are classified as intersecting lines