Question

Are triangles DEF and LNM similar if DF = 8 and LM = 4?

Answer 1

No, there is not enough information

Explanation:

Answer 2

We Cannot conclude that triangles DEF and LNM are similar if DF = 8 and LM = 4.

Solution:

Given that for two triangle DEF and LNM, DE = 8 and LM = 4.

To say that two triangles are similar the provided information is not complete.

Two triangles DEF and LNM , will be similar if there corresponding sides are in ratio which means

`\frac{\mathrm{DE}}{\mathrm{LM}}=\frac{\mathrm{EF}}{\mathrm{NM}}=\frac{\mathrm{EF}}{\mathrm{NM}}`

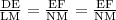
But we have only information of
`\frac{\mathrm{DE}}{\mathrm{LM}}=(8)/(4)=2`

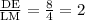
But do not have any information regarding two remaining ratios that are
`\frac{\mathrm{EF}}{\mathrm{NM}} \text { and } \frac{\mathrm{EF}}{\mathrm{NM}}`

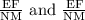
Hence cannot conclude that triangles DEF and LNM similar if DF = 8 and LM = 4