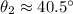Answer:
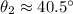
Step-by-step explanation:
Given:
velocity of the ball first and ball second,
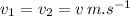
angle of projection of the first ball,

∵The balls should land at the same point,
∴their range of projectile,
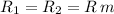
As we know for the range of projectile:
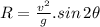
∵ we have equal range in both the cases
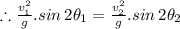
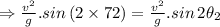
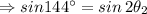
![2\theta_2=sin^(-1)[sin 144^(\circ)]](https://img.qammunity.org/2020/formulas/physics/high-school/avvwqup56t5i8njauqew0ul5ebsx3zrbm7.png)
![\theta_2=(1)/(2)* sin^(-1)[sin 144^(\circ)]](https://img.qammunity.org/2020/formulas/physics/high-school/7zsu6bvpwloomxvagj9rxjnucvaj7iho0w.png)