Question

On an examination given to students at a large number of different schools, the mean grade was 74.5 and thestandard deviation was 8.0. At one particular school where 200 students took the examination, the mean gradewas 75.9. Discuss the significance of this result at a 0.05 level from the viewpoint of (a) a one-tailed test, (b) atwo-tailed test, explaining carefully your conclusions on the basis of these tests

Answer 1

Reject Test.

Explanation:

Our values are:

`n=200`

`\sigma = 8`

`\mu = 74.5`

`\bar{x} = 75.9`

`\alpha=0.05 \rightarrow z_(c2)=1.96, z_(c1)=1.64`

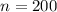
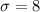
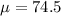
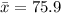
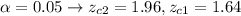
We have here a Null Hypothesis of
`H_0 : \mu \\eq  74.5`

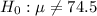
We calculate Z through Test Statistic,

`Z= \frac{\bar{x}-\mu}{\sigma/√(n)}`

`Z=(75.9-74.5)/(8√(200))`

`Z=2.4748`

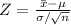
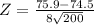
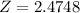
We can make now the comparation between our value with the critical value of Z_c = 1.96

a)
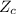`Z_c` = 1.64 at one tailed test,

Therefore
`|Z|>|Z_c|`
`\Rightarrow` we reject H_0

b)
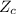`Z_c`= 1.96 at two tailed test

Therefore
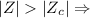`|Z|>|Z_c| \Rightarrow` we reject H_0

In this way the population mean
`\mu \\eq 74.5`

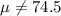
We can comprobate that both these test reject the null hypothesis