Question

Water at 25°C and 1 atm is flowing over a long flat plate with a velocity of 14 m/s. Determine the distance from the leading edge of the plate where the flow becomes turbulent, and the thickness of the boundary layer at that location. The density and dynamic viscosity of water at 1 atm and 25°C are rho = 997 kg/m3 and μ = 0.891 × 10–3 kg/m·s.

Answer 1

L=31.9 mm

δ = 0.22 mm

Step-by-step explanation:

Given that

v= 14 m/s

ρ=997 kg/m³

μ= 0.891 × 10⁻3 kg/m·s

As we know that when Reynolds number grater than 5 x 10⁵ then flow will become turbulent.

`Re=(\rho vL)/(\mu)`

`L=(Re\mu)/(\rho v)`

`L=(5* 10^5* 0.891* 10^(-3))/( 14 * 997)\ m`

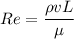
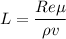
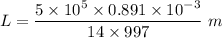
L=0.0319 m

L=31.9 mm

The thickness of the boundary layer at that location L given as

`\delta =(5L)/(√(Re))`

`\delta =(5*0.0319)/(√(5* 10^5))`

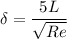
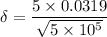
δ = 0.00022 m

δ = 0.22 mm