Answer:
The number of cubes that fill the prism is 24
Explanation:
Given as :
The length of cube (l) =
 cm
cm
The length of prism (L) = 1 cm
The width of prism (w) = 2
 =
=
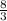 cm
cm
The height of prism (h) =
 cm
cm
Let the number of cubes that fill the prism = x
Now, Volume of cube with length (l) = l³ cm³
Or, Volume of cube with length (l) =
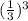 cm³
cm³
Or, Volume of cube with length (l) =
 cm³
cm³
Again , Volume of prism =
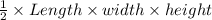
Or, Volume of prism =
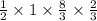
Or, Volume of prism =
 cm³
cm³
So , The number of cubes to fill prism
The number of cubes × Volume of cube = Volume of prism
Or, x ×
 cm³ =
cm³ =
 cm³
cm³
or x =
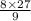 = 24
= 24
Hence The number of cubes which fill the prism is 24 Answer