Question

The international space station has a mass of 4.2 x 105 kg and it orbits the Earth at an average altitude of 400 km above the Earth’s surface. The radius of the Earth is 6400 km, and the mass of the Earth is 6.0 x 1024 kg. Assume the only force acting on the space station is the Universal Gravitational Force, FG, and assume that the orbit is perfectly circular. How long would it take for the space station to make one complete orbit around the Earth given these assumptions?

Answer 1

92.82253 minutes

Step-by-step explanation:

R = Radius of Earth = 6400000 m

h = Altitude of space station = 400000

r = R+h = 6400000+400000 m

M = Mass of Earth = 6 × 10²⁴ kg

m = Mass of satellite = 4.2×10⁵ kg

T = Time to complete one revolution

As centripetal force and gravitational force are conserved

`mr\omega^(2)=G(mM)/(r^(2))\\\Rightarrow mr\left({\frac {2\pi}{T}}\right)^(2)=G(mM)/(r^(2))\\\Rightarrow T=\sqrt{(4\pi^2r^3)/(GM)}`

`T=\sqrt{(4\pi^2* (6400000+400000)^3)/(6.67* 10^(-11)* 6* 10^(24))}\\\Rightarrow T=5569.35235\ seconds=92.82253\ minutes`

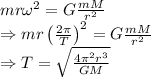
The time it takes for the space station to make one complete orbit around the Earth is 92.82253 minutes