Answer:
The larger sample sizes gives a narrower confidence interval
Explanation:
The larger sample sizes gives a narrower confidence interval, that is, a more "precise" estimation of the elections results.
In a confidence interval of proportions, we have that the lower end is given by:
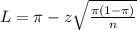
In which
 is the probability of a sucess,
is the probability of a sucess,
 is a value from the Z table and n is the length of the sample.
is a value from the Z table and n is the length of the sample.
The upper end is given by:

As n increases, the difference between U and L decreases. This means that the confidence interval gets narrower.