The power generated is about
 Watt when the waterfall from the waterfall and reaches the bottom.
Watt when the waterfall from the waterfall and reaches the bottom.
Step-by-step explanation:
As per given question, the rate of water is
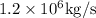
From height (h) of 50m and acceleration due to gravity is 9.8
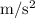
we know that Potential Energy,
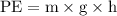
The potential energy of
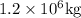 (m) water for one second is written as
(m) water for one second is written as
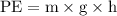
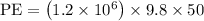

But power output of 1 Watt = 1 Joule / second. So the power generated in the waterfall is
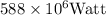 or we can also write as 588 Mega Watts.
or we can also write as 588 Mega Watts.