Question

A highway engineer wants to estimate the maximum number of carsthat can safely travel on a particular road at a given speed. Heassumes that each car is 17 feet long, travels at speeds, and follows the car in front of it at a safedistance for that speed. He finds that the number N ofcars that can pass a given spot per minute is modeled by thefunction

N (s) = (81s) /(17+17(s/20)^2)
At what speed can the greatest number of cars travel safely on thatroad?

Answer 1

s=4

Explanation:

you have to get the derivative by minimizing speed

Answer 2

s = 20 ft/s

Explanation:

Given:-

- The relationship between the N of cars that can pass a given spot per minute is modeled by the function:

`N(s) = (81s)/(17 + 17*((s)/(20))^2 )`

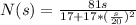
Where , s = speed of the car.

Find:-

At what speed can the greatest number of cars travel safely on that road?

Solution:-

- To maximize the number of cars (N) that travel safely on the road we will take derivative of the given function as follows and find the critical value(s) at which (N) maximizes / minimizes.

`N(s) = 81*(s)/(17 + ((17*s^2)/(400)) )\\\\N'(s) = 81* [ (( 17 + (17s^2)/(400)) - s*( (2s*17)/(400) + 0 ))/(((17*s^2)/(400) + 17 )^2) ]\\\\N'(s) = 81* [ (( 17 - (17s^2)/(400)) )/(((17*s^2)/(400) + 17 )^2) ] = - (32400(s^2 - 400))/(17(s^2 + 400)^2)`

- Now set the first derivative N'(s) equal to zero and solve for "s":

`N'(s) = - (32400(s^2 - 400))/(17(s^2 + 400)^2) = 0\\\\(s^2 - 400) = 0\\\\s = √(400) = 20`

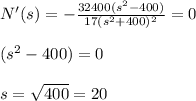
- So the maximum number of cars (N) that travel safely on the road we would have a speed of s = 20 ft/s.