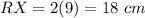Answer:
Option D. 18 cm
Explanation:
we know that
A centroid of a triangle is the point where the three medians of the triangle meet.
A median of a triangle is a line segment from one vertex to the mid point on the opposite side of the triangle.
The centroid divides each median in a ratio of 2:1
In this problem the centroid of triangle RST is the point X
so
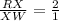
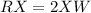 -----> equation A
-----> equation A
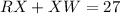 -----> equation B
-----> equation B
substitute equation A in equation B
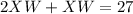
Solve for XW
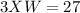
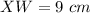
Find the value of RX
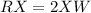 -----
-----