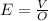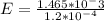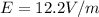Question

In the steady state 1.2 ✕ 1018 electrons per second enter bulb 1. There are 6.3 ✕ 1028 mobile electrons per cubic meter in tungsten. The cross-sectional area of the tungsten filament in bulb 1 is 1.3 ✕ 10-8 m2. The electron mobility in hot tungsten is 1.2 ✕ 10-4 (m/s)/(N/C). Calculate the magnitude of the electric field inside the tungsten filament in bulb 3.

Answer 1

E=12.2V/m

Step-by-step explanation:

To solve this problem we must address the concepts of drift velocity. A drift velocity is the average velocity attained by charged particles, such as electrons, in a material due to an electric field.

The equation is given by,

`V=(I)/(nAq)`

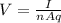
Where,

V= Drift Velocity

I= Flow of current

n= number of electrons

q = charge of electron

A = cross-section area.

For this problem we know that there is a rate of 1.8*10^{18} electrons per second, that is

`(I)/(q) = 1.2*10^(18)`

`A= 1.3*10^(-8)m^2`

`n=6.3*10^(28) e/m^3`

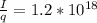
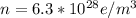
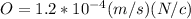`\omicron{O} = 1.2*10^(-4)(m/s)(N/c)` Mobility

We can find the drift velocity replacing,

`V = (1.2*10^(18))/((1.3*10^(-8))(6.3*10^(28)))`

`V= 1.465*10^-3m/s`

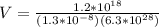
The electric field is given by,

`E= \frac{V}{\omicron{O}}`

`E=(1.465*10^-3)/(1.2*10^(-4))`

`E=12.2V/m`