Answer: 0.2858
Explanation:
Given : When fishing off the shores of Florida, a spotted seatrout must be between 24 and 30 inches long before it can be kept.
In a region of the Gulf of Mexico, the lengths of the spotted seatrout that are caught, are normally distributed with
 and
and
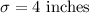 .
.
Let x be the lengths of the spotted seatrout that are caught .
Using formula

For x= 24
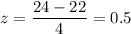
For x= 30
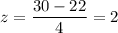
Then, by using the z-value table , the probability that a fisherman catches a spotted seatrout within the legal limits will be :-
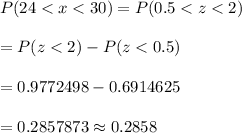
Hence, the probability that a fisherman catches a spotted seatrout within the legal limits = 0.2858