Question

The average daily temperature, t, in degrees Fahrenheit for a city as a function of the month of the year, m, can be modeled by the equation t=35cos(pi/6(m+3))+55, where m = 0 represents January 1, m = 1 represents February 1, m = 2 represents March 1, and so on. Which equation also models this situation?

A) t=-35sin(pi/6m)+55

B) t=-35sin(pi/6(m+3))+55

C) t=35sin(pi/6m)+55

D) t=35sin(pi/6(m+3))+55

Answer 1

A

Explanation:

edge

Answer 2

Answer is A.

Explanation:

For the equation: 35cos(pi/6(m+3)+55)

Simplify it by multiplying pi/6 in the bracket values:

`=35cos((m.pi)/(6)+(3.pi)/(6)+55) \\=35cos((m.pi)/(6)+55+(pi)/(2))`

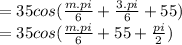
Now suppose x = m.pi/6+55, while pi/2 = 90⁰

As per law cos(x+90⁰)=-sin(x)

so,

cos((m.pi/6)+55+90⁰=-sin((m.pi/6)+55)

Hence answer will be

`=-35sin((m.pi)/(6)+55)`

.

The law cos(x+90⁰)=-sin(x) can be proved by putting y=90⁰ in the following formula,

cos(x+y)=cos(x).cos(y)-sin(x).sin(y)