Answer with explanation:
As per given , we have
n= 1025
x=707
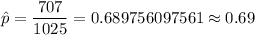
Critical value for 99% confidence interval :
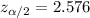
Confidence interval :
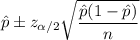
i.e.

i.e.
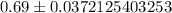
i.e.
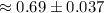
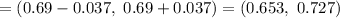
99% confidence interval for the proportion of all U.S. adults in December of 2012 who were optimistic about their finances in 2013= (0.653, 0.727)
Interpretation : We are 99% confident that the true population of all U.S. adults in December of 2012 who were optimistic about their finances in 2013 lies in interval (0.653, 0.727).