Answer:
307 is an inverse of 43 mod 660
Explanation:
We know that given integers
 and
and
 , if
, if
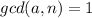 , then
, then
 has an inverse modulo
has an inverse modulo
 , and using Euclidean algorithm we find an inverse of
, and using Euclidean algorithm we find an inverse of
 expressing 1 as a linear combination of
expressing 1 as a linear combination of
 and
and
 finding integers
finding integers
 and
and
 such that
such that
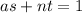 , in this case,
, in this case,
 is an inverse of
is an inverse of
 , i.e.,
, i.e.,
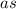 ≡
≡
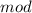
To find the inverse of 43 mod 600, we need to do two steps:
- We need to calculate the Greatest Common Divisor of 660 and 43 (gcd(660, 43)) using the Euclidean algorithm and verify that gcd(a, n) = 1.
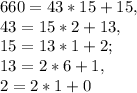
which implies that gcd(660, 43)= 1 and so 660 and 43 are relatively prime.
2. Express 1 as a linear combination of 43 and 600.
We work backwards using the equations derived by applying the Euclidean algorithm, expressing each remainder as a linear combination of the associated divisor and dividend:
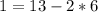
 substitute
substitute
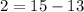 ,
,
 by algebra
by algebra
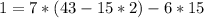 substitute
substitute

 by algebra
by algebra
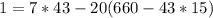 substitute
substitute

 by algebra.
by algebra.
Thus 43*307=1+20*660, then by definition of congruence modulo 660, 43*307 ≡ 1 (mod 600) and therefore 307 is an inverse of 43 mod 660.