Question

4x^2 - 6x + 2 = 0

a. find the value of the discriminate
b. find the exact solutions by using the quadratic formula.
please show steps.​

Answer 1

a. Discriminant = 4

b. x = 1 and
`x = (1)/(2)`

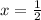
Explanation:

The Sridhar Acharya Formula gives if ax² + bx + c = 0, the then the roots of the equation is given by

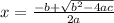`x = \frac{-b +\sqrt{b^(2)-4ac } }{2a}` and
`x = \frac{-b -\sqrt{b^(2)-4ac } }{2a}`

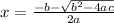
In this solution the term
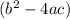`(b^(2) -4ac)` is called the discriminant of the original quadratic equation.

Now, in our case the equation is 4x² - 6x + 2 = 0

a. Therefore, the discriminant of this equation is = (-6)² - 4 × 4 × 2 = 4

b. The solutions of the equation are

`x= (-(-6) +√(4) )/(2 * 4)=1`

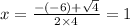
and
`x= (-(-6) -√(4) )/(2 * 4)=(1)/(2)` (Answer)