Question

Find the solution of the given initial value problem in explicit form. y' = (1 – 11x)y?, y(0) = -1 Enclose numerators and denominators in parentheses. For example, (a - b)/(1 + n). y(x) = Q

Answer 1

`y(x)=-e^{x-((11*x^(2) )/(2)) }`

Explanation:

This is a separable equation. First divide both sides by y:

`(dy(x))/((dx)/(y(x)) ) =-11x+1\\(dy)/(y)=(-11x+1)dx`

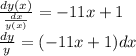
Integrate both sides:

`\int\ (dy)/(y) \ =\int\ (-11x+1) \, dx`

`log(y)=-((11*x)/(2) )+x+ c_1`

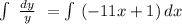
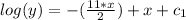
Solve for y taking exp to both sides:

`y(x)=c_1*e^{x-((11*x^(2) )/(2)) }`

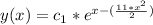
Where
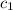`c_1` is an arbitrary constant

Evaluating the initial condition:

`y(0)=c_1*e^{0-((11*0^(2) )/(2)) } =-1`

`c_1*e^(0) =-1\\c_1*1=-1\\c_1=-1`

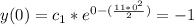
Finally, replacing
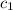`c_1` in the differential equation solution:

`y(x)=-e^{x-((11*x^(2) )/(2)) }`