Question

a person pushing a stroller starts from rest, uniformly accelerating at a rate of 0.500 m/s2. What is the velocity of the stroller after it has traveled 4.75 m ?

Answer 1

Approximately
`2.18 m\cdot s^(-1)`.

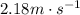Step-by-step explanation:

Consider one of the equations for constant acceleration ("SUVAT" equations)

`v^(2) - u^(2) = 2 \; a \cdot x`,

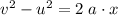where

• 
  `v` is the final velocity of the object,
• 
  `u` is the initial velocity of the object,
• 
  `a` is the acceleration of the object, and
• 
  `x` is the distance that the object had traveled while its velocity changed from
  `u` to
  `v`.

Note that unlike other SUVAT equations, this one does not ask for the time required for the speed of the object to change from
`u` to
`v`. Since in this problem, time isn't given, this time-less equation would particular useful.

Here

• 
  `v` the final velocity needs to be found.
• 
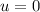  `u = 0` for the stroller started from rest.
• 
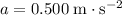  `a =\rm 0.500 \;m \cdot s^(-2)` is the acceleration of the stroller, and
• 
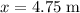  `x = \rm 4.75\; m` is the distance that the stroller traveled while its velocity changed from
  `u` to
  `v`.

Rearrange the equation to isolate the unknown,
`v`:

`v^(2) = u^(2) + 2 \; a \cdot x`.

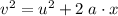Make sure that all units are standard, so that the unit of the output will also be standard. Apply the equation:

`v = \sqrt{u^(2) + 2 \; a \cdot x} = √(0^2 + 2 * 0.500 * 4.75 )\approx \rm 2.18\; m\cdot s^(-1)`.

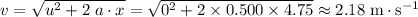Hence the final velocity will be approximately
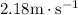`\rm 2.18 m\cdot s^(-1)`.