Question

In triangle RSW, line segment RW is a median and is equal to 27 cm. What is the length of RX?

13.5cm
9cm
27cm
18cm

Answer 1

Answer: LAST OPTION.

Explanation:

By definition the line segment that goes from a vertex of the triangle to the midpoint of the oposite side, is called "Median of a triangle".

The medians of a triangle intersect at point called "The centroid of the triangle" and this divides each median in a ratio
`2:1`.

In this case, you can notice that the Centroid of the given triangle is the point "X".

Based on the explained before, we can write the following porportion:

`(RX)/(XW)= (2)/(1)`

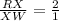
Solving for "XW":

`XW=(RX)/(2)`

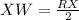
Since the lenght of "RX" is 27 centimeters, you know that;

`RX+XW=27`

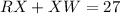
Substituting
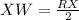`XW=(RX)/(2)` into
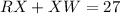`RX+XW=27` and solving for "RX", we get that its lenght is:

`RX+(RX)/(2)=27\\\\(3)/(2)RX=27\\\\RX=(27)((2)/(3))\\\\RX=18\ cm`