Question

A blimp can be seen flying at an altitude of 5500 feet above a motor speedway during a race. The slanted distance directly to the pagoda at the startdashfinish line is d feet. Express the horizontal distance h as a function of d.

Answer 1

The expression of h as function of x is h =
`√((d + 5500) (d - 5500))`

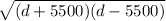
Explanation:

Given as :

The distance of blimp (AB) = 5500 feet

The slanted distance to the pagoda (BC) = d feet

The horizontal distance (AC) = h

Let the angle made between slanted distance and horizontal distance be Ф

So , cos Ф =
`(AC)/(BC)` =
`(h)/(d)`

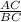And sin Ф =
`(AB)/(BC)` =
`(5500)/(d)`

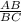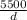
∵, cos²Ф = 1 - sin²Ф

So,
`((h)/(d))^(2)` =
`1 - ((5500)/(d))^(2)`

Or,
`((h)/(d))^(2)` =
`((d^(2)- 5500^(2))/(d^(2)))`

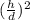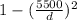
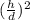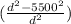
Or, h² = d² - 5500²

∴ h =
`\sqrt{d^(2)- 5500^(2)}`

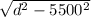
Or, h =
`√((d + 5500) (d - 5500))`

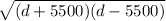
Hence The expression of h as function of x is h =
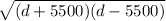`√((d + 5500) (d - 5500))` Answer