Question

A continuous and aligned fibrous reinforced composite having a cross-sectional area of 970 mm2 (1.5 in.2) is subjected to an external tensile load. If the stresses sustained by the fibre and matrix phases are 215 MPa (31,300 psi) and 5.38 MPa (780 psi), respectively, the force sustained by the fibre phase is 76,800 N (17,265 lbf), and the total longitudinal composite strain is 1.56 × 10–3, determine the following:

(a) The force sustained by the matrix phase

(b) The modulus of elasticity of the composite material in the longitudinal direction

(c) The moduli of elasticity for fibre and matrix phases

Answer 1

(a) 3290 N

(b) 52.9 Gpa

(c) 3.45 Gpa and 1378 Gpa for matrix and fibre phases respectively

Step-by-step explanation:

(a)

The volume fraction of matrix is given by

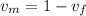`v_m=1-v_f` where
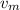`v_m` is volume fraction of matrix and
`v_f` is volume fraction of fibre

Moreover, the stress in matrix is given by

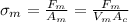`\sigma_m=\frac {F_m}{A_m}=\frac {F_m}{V_mA_c}` where
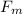`F_m` is force on matrix and
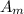`A_m` is the area of matrix,
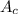`A_c` is cross-sectional area

Therefore,
`F_m=V_mA_c\sigma_m`

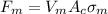
Substituting the figures in the question

`F_m=0.631*(0.970*10^(-3))*(5.38*10^(6))=3290 N`

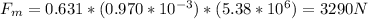
Therefore, force sustained by matrix is 3290 N

(b)

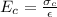`E_c=\frac {\sigma_c}{\epsilon}` and also

`\sigma_c=\frac {F_m+F_f}{A_c}` therefore we combine these two equations and say

`E_c=\frac {\sigma_c}{\epsilon}= \frac {F_m+F_f}{\epsilon A_c}`

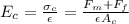
Substituting the figures given

`E_c=\frac {3290 N +76800 N}{(1.56*10^(-3)*(0.970*10^(-3))}=52.9*10^(9)=52.9 GPa`

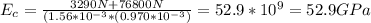
(c)

The moduli of elasticity of matrix and fibre are given by

`E_m=\frac {\sigma_m}{\epsilon_m}=\frac {\sigma_m}{\epsilon_c}`

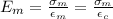
Therefore,

`E_m=\frac {5.38*10^(6)}{1.56*10^(-3)}=3.45*10^(9)=3.45 Gpa`

`E_f=\frac {215*10^(6)}{1.56*10^(-3)}=1.378*10^(11)=1378 Gpa`

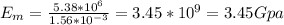
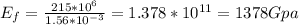
Therefore, moduli of elasticity for fibre and matrix phases are 1378 Gpa and 3.45 Gpa respectively