Question

A freezer compartment is covered with a 3-mm-thick layer of frost at the time it malfunctions. If the compartment is in ambient air at 20°C and a coefficient of LaTeX: h=\:2\:\frac{W}{m^2.K}h = 2 W m 2 . K characterized heat transfer by natural convection from the exposed surface of the layer, estimate the time required (in seconds) to completely melt the frost. The frost may be assumed to have a mass density of 700 LaTeX: \frac{kg}{m^3}k g m 3 and a latent heat of fusion of 334 kJ/kg.

Answer 1

3h12min

Step-by-step explanation:

We need to apply our thermodynamics concepts to find the required time in which the ice will melt at a given temperature.

In our data we have defined that,

`\rho_f = 700kg/m^3`

`hs_f = 334kJ/kg`

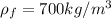
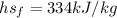
Performing an energy balance you have to:

`E_(in) - E_(out) = E_(T)`

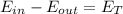
Internal energy is given by,

`qA_sdt = dU`

`A_s*h(T_(\infty)-T_f)dt = -\rho_f A_shs_fdx`

Integrating,

`h(T_(\infty)-T_f)\int\limit^(t_m)_0dt = -\rho_fhs_f\int^0_(x_0)dx`

`t_m = (\rho hs_fx_0)/(h(T_(\infty)-T_f))`

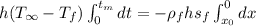
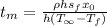
Replacing the values,

`t_m = ((700)(334*10^3)(0.002))/(2(20-0))`

`t_m = 11.690s`

`t_m \approx 3h12min`

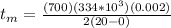
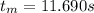
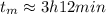
Note: It was assumed that fros is isothermal and the radiation exchange is also negligible.