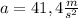Question

A 0.20-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 360 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is x = -2.3×10−2 m, find the acceleration of the block.

Answer 1

The answer is 41,4
`(m)/(s^(2))`

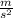
Step-by-step explanation:

To understand this problem we need to visualize when block is at the equilibrium position and when the displacement is x=
`-2,3.10^(-2)`.

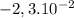According to Newton's law
`F=ma`, if we find the force applied to the block, we can find the acceleration since we know the mass of the block.

If you compress a spring by x displacement under F force, the spring's force can be found as:

`F_(spring) =kx`

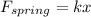
Therefore
`F=360(N)/(m) .2,3.12^(-2) =8,28N`

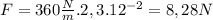
And to find acceleration:

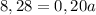`F=ma` →
`8,28=0,20a` →
`a=41,4(m)/(s^(2))`