Question

Triangle X Y Z is shown. Angle X Z Y is a right angle. Angle Z X Y is 60 degrees and angle X Y Z is 30 degrees. The length of hypotenuse X Y is 4. Given right triangle XYZ, what is the value of tan(Y)? One-half StartFraction StartRoot 3 EndRoot Over 3 EndFraction StartFraction StartRoot 3 EndRoot Over 2 EndFraction StartFraction 2 StartRoot 3 EndRoot Over 3 EndFraction

Answer 1

B.

Explanation:

took the test on edge, hope this helps

Answer 2

StartFraction StartRoot 3 EndRoot Over 3 EndFraction

Explanation:

see the attached figure to better understand the problem

step 1

we know that

In the right triangle XYZ

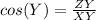`cos(Y)=(ZY)/(XY)` ---> adjacent side divided by the hypotenuse

substitute the values

`cos(30\°)=(ZY)/(4)`

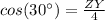
Remember that

`cos(30\°)=(√(3))/(2)`

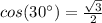
so

substitute

`(√(3))/(2)=(ZY)/(4)`

`ZY=(4)(√(3))/(2)`

`ZY=2√(3)\ units`

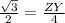
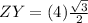
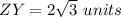
step 2

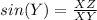`sin(Y)=(XZ)/(XY)` --> opposite side divided by the hypotenuse

substitute the values

`sin(30\°)=(XZ)/(4)`

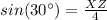
Remember that

`sin(30\°)=(1)/(2)`

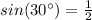
so

`(1)/(2)=(XZ)/(4)`

`XZ=2\ units`

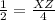
step 3

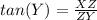`tan(Y)=(XZ)/(ZY)` --> opposite side divided by adjacent side

substitute the values

`tan(Y)=(2)/(2√(3))`

`tan(Y)=(1)/(√(3))`

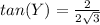
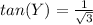
Simplify

`tan(Y)=(√(3))/(3)`

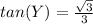
so

StartFraction StartRoot 3 EndRoot Over 3 EndFraction