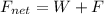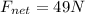Question

A box is put on a scale that is adjusted to read zero when the box is empty. A stream of marbles is then poured into the box from a height h above its bottom at a rate of R (marbles per second). Each marble has mass m. The collisions are completely inelastic; assume that the marbles stick to the box without bouncing when they hit. Find the scale reading at time t after the marbles begin to fill the box. Determine a numerical answer when R = 120 s-1, h = 7.80 m, m = 4.50 g, and t = 8.0 s.

Answer 1

`F_(net) = 49 N`

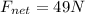
Step-by-step explanation:

As we know that rate of marble that strike the target is given as

`R = 120 per s`

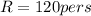
now we know that after t = 8 s total marbles that accumulated in the box is given as

`N = Rt`

`N = 120(8)`

`N = 960`

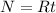
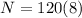
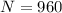
now total weight of the marbles is given as

`W = N(mg)`

`W = 960(4.5 * 10^(-3))(9.81)`

`W = 42.37 N`

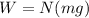
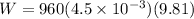
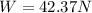
Now force due to impact of marble is given as

`F = (dN)/(dt)mv`

`v = √(2gh)`

`v = √(2(9.81)(7.80)) = 12.37 m/s`

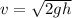
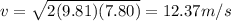
now we have

`F = 120(4.5 * 10^(-3))(12.37)`

`F = 6.68 N`

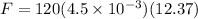
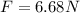
so total force on the box is given as

`F_(net) = W + F`

`F_(net) = 42.37 + 6.68`

`F_(net) = 49 N`