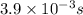Question

Some bacteria are propelled by motors that spin hair-like flagella. A typical bacterial motor turning at a constant angular velocity has a radius of 1.3 x10-8m, and a tangential speed at the rim of 2.1 x10-5 m/s. (a) What is the angular speed (the magnitude of the angular velocity) of this bacterial motor? (b) How long does it take the motor to make one revolution?

Answer 1

(a) The angular speed of this bacterial motor is
`1.6* 10^3s^(-1)`

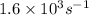
(b) The time taken by the motor to make one revolution is
`3.9* 10^(-3)s`

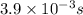
Explanation :

(a) To determine the angular speed of this bacterial motor.

Angular speed : It is defined as the rate at which an object changes its angle.

Formula used :

`\omega=(v)/(r)`

where,

`\omega` = angular speed

v = tangential speed =
`2.1* 10^(-5)m/s`

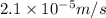
r = radius =
`1.3* 10^(-8)m`

Now put all the given values in the above formula, we get:

`\omega=(2.1* 10^(-5)m/s)/(1.3* 10^(-8)m)`

`\omega=1.6* 10^3s^(-1)`

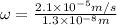
Thus, the angular speed of this bacterial motor is
`1.6* 10^3s^(-1)`

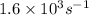
(b) to determine the time taken by the motor to make one revolution.

Formula used :

`T=(2\pi)/(\omega)`

where,

T = time

Now put all the given values in this formula, we get:

`T=(2* 3.14)/(1.6* 10^3s^(-1))`

`T=3.9* 10^(-3)s`

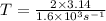
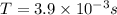
Thus, the time taken by the motor to make one revolution is
`3.9* 10^(-3)s`