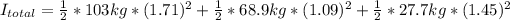Question

A 103 kg horizontal platform is a uniform disk of radius 1.71 m and can rotate about the vertical axis through its center. A 68.9 kg person stands on the platform at a distance of 1.09 m from the center, and a 27.7 kg dog sits on the platform near the person 1.45 m from the center. Find the moment of inertia of this system, consisting of the platform and its population, with respect to the axis.

Answer 1

`I_(total)=220.64 kg*m^(2)`

Step-by-step explanation:

The moment of inertia of the system is equal to the each population and the platform inertia so

Inertia disk

`I_(disk)=(1)/(2)*m_(disk)*(r_(p))^(2)`

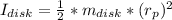
Inertia person

`I_(p)=(1)/(2)*m_(p)*(r_(p))^(2)`

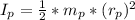
Inertia dog

`I_(d)=(1)/(2)*m_(d)*(r_(d))^(2)`

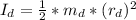
The Inertia of the system is the sum of each mass taking into account that all exert the force of inertia:

`I_(total)=I_(disk)+I_(p)+I_(d)`

`I_(total)=(1)/(2)*103kg*(1.71)^(2)+(1)/(2)*68.9kg*(1.09)^(2)+(1)/(2)*27.7kg*(1.45)^(2)`

`I_(total)=220.64 kg*m^(2)`