Answer:
37,800
Explanation:
The word ''knickknack'' has repetition, so, rearrangements with repetitions are calculated with the formula

n is the total number of letter.
Letters above r, s and t, refers to the number of repetitions, in this case 3 letter repeat: k, n and c.
So, applying all this we have:

So, there are 10 letter, k repeats 4 times, n and c repeat twice
The sign ''!'' means that is a factorial operation, which is solved multiplying in a regressive way, for example: 4! = 4x3x2x1.
Then,
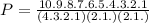
Solving all, we have:
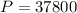
Therefore, there are 37800 ways to rearrange the letter of the word ''knickknack''