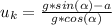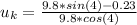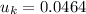Question

A ski that is placed on snow will stick to the snow. However, when the ski is moved along the snow, the rubbing warms and partially melts the snow, reducing the coefficient of friction and promoting sliding. Waxing the ski makes it water repellent and reduces friction with the resulting layer of water. A magazine reports that a new type of plastic ski is especially water repellent and that, on a gentle 200 m slope in the Alps, a skier reduced his top-to-bottom time from 47.94 s with standard skis to 33.94 s with the new skis. Determine the magnitudes of his average acceleration with each pair of skis. Acceleration with old model ski? Acceleration with new model ski? Assuming a 4.0° slope, compute the coefficient of kinetic friction for each case. Old model ski coefficient of friction? New model ski coefficient of friction?

Answer 1

a). Acceleration with old model
`a_(o)=8.343(m)/(s^(2))`

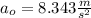
b). Acceleration with new model
`a_(n)=11.785(m)/(s^(2))`

c). Coefficient of kinetic friction old model
`u_(k)=0.0515`

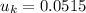
d). Coefficient of kinetic friction old model
`u_(k)=0.0464`

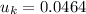
Step-by-step explanation:

Using the Newton laws so the initial speed is zero

so:

Δ
`x=v_(o)*t+(1)/(2)*a*t^(2)`

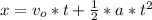
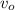`v_(o)` because the ski began from the rest initial velocity is zero

Δ
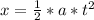
`x=(1)/(2)*a*t^(2)`

a).

`a=(2*x)/(t^(2))`

`a_(o)=(2*200m)/((47.94s)^(2))`

`a_(o)=8.343(m)/(s^(2))`

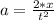
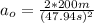
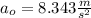
b).

`a=(2*x)/(t^(2))`

`a_(n)=(2*200m)/((33.94s)^(2))`

`a_(n)=11.785(m)/(s^(2))`

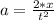
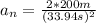
In the horizontal direction the friction force acts on the ski is:

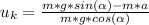
`f_(k)=u_(k)*m*g*cos(\alpha)`

`u_(k)=(m*g*sin(\alpha)-m*a)/(m*g*cos(\alpha))`

c).

`u_(k)=(g*sin(\alpha)-a)/(g*cos(\alpha))`

`u_(k)=(9.8*sin(4)-0.108)/(9.8*cos(4))`

`u_(k)=0.0515`

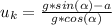
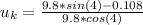
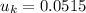
d).

`u_(k)=(g*sin(\alpha)-a)/(g*cos(\alpha))`

`u_(k)=(9.8*sin(4)-0.23)/(9.8*cos(4))`

`u_(k)=0.0464`