Answer:
(-4, 17) and (5.-28)
(-6, 14) and (4.-16)
(-2.16) and (2.-20)
Explanation:
we know that
If two lines intersect, then their slopes are different
The formula to calculate the slope between two points is equal to
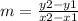
Find the slope of the given line
points (-2, 12) and (3, -23)
substitute in the formula
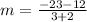
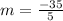
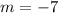
Verify each case
case 1
(-3, 19) and (6.-44)
substitute in the formula
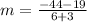
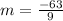
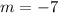
Compare with the slope of the given line
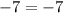
The slopes are the same
therefore
The lines not intersect because are parallel lines
case 2
(-5,32) and (3.-24)
substitute in the formula
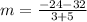
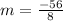
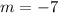
Compare with the slope of the given line
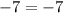
The slopes are the same
therefore
The lines not intersect because are parallel lines
case 3
(-4, 17) and (5.-28)
substitute in the formula
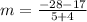
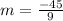
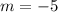
Compare with the slope of the given line
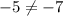
The slopes are different
therefore
The lines intersect
case 4
(-6, 14) and (4.-16)
substitute in the formula
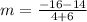
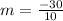
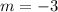
Compare with the slope of the given line
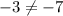
The slopes are different
therefore
The lines intersect
case 5
(-2.16) and (2.-20)
substitute in the formula
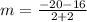
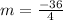
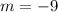
Compare with the slope of the given line
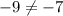
The slopes are different
therefore
The lines intersect