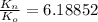Answer:
77.76729 rad/s or 12.37704 rev/s
Step-by-step explanation:
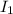 = Rotational inertia of the system consisting of the man, bricks, and platform about the central axis = 7.55 kgm²
= Rotational inertia of the system consisting of the man, bricks, and platform about the central axis = 7.55 kgm²
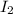 = Decreased the rotational inertia of the system = 1.22 kgm²
= Decreased the rotational inertia of the system = 1.22 kgm²
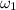 = Angular velocity of the old system =
= Angular velocity of the old system =

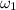 = Angular velocity of the new system
= Angular velocity of the new system
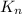 = Kinetic energy of the new system
= Kinetic energy of the new system
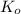 = Kinetic energy of the old system
= Kinetic energy of the old system
Here, angular momentum is conserved
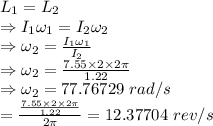
The resulting angular speed of the platform is 77.76729 rad/s or 12.37704 rev/s
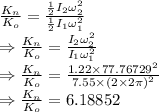
The ratio of the new kinetic energy of the system to the original kinetic energy is