Question

In a basketball game, a ball leaves a player's hand 6.1 m

downrange from the basket from a height of 1.2 m

below the level of the basket. If the initial velocity of

the ball is 7.8 m/s [55° above the horizontal] in line

with the basket, will the player score a basket? If not,

by how much will the ball miss the basket?

Answer 1

The player won't score and will miss the basket for 2.07m short.

Step-by-step explanation:

We have a 2D proyectile problem, the basketball is moving at the same time in the X and Y axes, we can start by writing the information given:

The distance between the player and the basket is 6.1m that will be X.

The height where the basket was launched is 1.2m that will be the initial position or
`Y_(0)`.

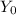The initial velocity,
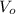`V_(o)` is 7.8 m/s and its launched within 55° with the horizontal, that will be α.

We also need the equations of 2D movemnt

`1. X=X_(0) +V_(x) *t\\2. Y=Y_(0) +V_(0Y) *t+(1)/(2)*a_(y) *t^(2)\\3. V_(x)=V_(0)*cos(\alpha)\\4. V_(y)=V_(0)*sin(\alpha)`

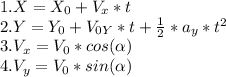
We can find the flying time t by using (1)

`t=(X-X_(0) )/(V_(0)*cos(\alpha))`

`t=1.36s`

We can replace t in (2) and find what would be Y with that flying time, if it is equal to 3.05m the height of a basket the player would score, but if not he'll miss.

`Y=0.83m`

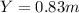
As
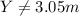`Y\\eq 3.05m` the player won't score so we need to find how much will the ball miss the basket.

Using Y as 3.05m we can find the flying time necessary to score with equation 2.

we would obtain 2 answers for t, we have to chose the second one, remember that in a parabolic movement you pass 2 times through the same hight when you are going up and when you are going down so after finding the answers
`t=0.87s`.

Finally replacing t found just before in (1) we can find the actual X, we will call it
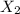`X_(2)` distance that the ball will travel.

`X_(2)=3.93m`

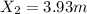
and subtracting the two distances we will find by how much the ball will miss the basket.

`X-X_(2)=2.07m`

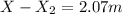
So the player will miss the basket for 2.07 m.