Answer:
We just need to evaluate and get f(2i)=0, f(-2i)=0.
Explanation:
Since
 , then
, then
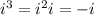 , and we can apply this when we evaluate
, and we can apply this when we evaluate
 for 2i and -2i.
for 2i and -2i.
First we have:
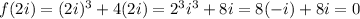
Which shows that 2i is a zero of f(x).
Then we have:
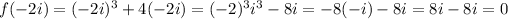
Which shows that -2i is a zero of f(x).