Answer:

Explanation:
Let x denotes the total number of pages in Jack's book , then we have
Then, the fraction of book he studies on Monday =
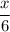
Fraction of book he studies on Tuesday =
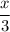
The remaining pages of book he studied in 4 days =
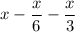
Simplify using LCM, we get
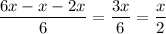
i.e. The remaining pages of book he studied in 4 days =

i.e. Fraction of the book he read on 4 days =

Then, the fraction of the book he read on each of the 4 days =
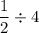
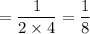
Hence, Fraction of the book he read on each of the 4 days =
