Question

The resistance in ohms of a metal wire temperature sensor varies directly as the temperature in degrees Kelvin​ (K). If the resistance is 510 ohms at a temperature of 170 ​K, find the resistance at a temperature of 250 K?

Answer 1

The resistance at a temperature of 250 K is 750 ohms

Explanation:

We know that the resistance of a metal wire temperature sensor varies directly as the temperature, so we can construct a model using direct variation.

The definition of direct variation is:

Let x and y denote two quantities. Then y varies directly with x, or y is directly proportional to x, if there is a nonzero number k such that

`y=kx`

The number k is called the constant of proportionality.

Applying the definition of direct variation to our situation, we get

Let R be the resistance in ohms, and t the temperature in K

`R=kt`

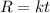
Next, find the value of k, we know that when the temperature is 170 K the resistance is 510 ohms

`510=k\cdot 170\\\\k=(510)/(170)=3\:(ohms)/(K)`

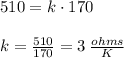
Substitute k into the equation

`R=3\cdot t`

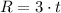
Find the resistance at a temperature of 250 K

`R=3\cdot 250=750 \:ohms`

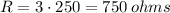
The resistance at a temperature of 250 K is 750 ohms.