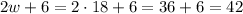Question

What is the measurement of STU?

Answer 1

Triangles UTR and RTS are congruent, because they're both right triangles, RS=RU and side TR is in common.

This implies that angles RTS and RTU are congruent, and thus we have

`5w-69=w+3 \iff 4w=72 \iff w=(72)/(4)=18`

Finally, angle STU is the sum of RTS and RTU, which is the same as 2RTU, since they have the same measure. So, we have

`RTS+RTU=2RTU=2(w+3)=2w+6`

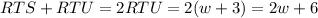
and since w=18, we have

`2w+6=2\cdot 18+6=36+6=42`