The function is

since she pays $80 flat, and then $0.2 for each text message.
This implies that
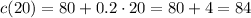
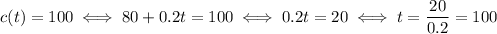
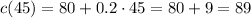

For the last question, we have to see how many texts it takes to pay $20: we have
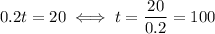
So, if she sends less than 100 texts a month, it is more convenient to pay $0.2 for each text. If the sends more than 100 texts a month, it is more convenient to pay a flat fee of $20 for unlimited messages.