First of all, let's consider the line, since it's simpler to graph: we draw the endpoints and connect them:
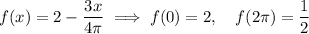
So, you just need to draw the points
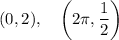
As for the trigonometric function, we have to start from the parent function
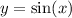 and derive the graph of its child function via transformations:
and derive the graph of its child function via transformations:
- When we multiply the whole function by 2, we stretch the graph vertically. So, the function has still period
 , but now it ranges from -2 to 2 instead of from -1 to 1 (amplitude 2)
, but now it ranges from -2 to 2 instead of from -1 to 1 (amplitude 2) - When we multiply the argument by 2, we compress the function horizontally. So, the new period becomes
 , and the function makes two complete oscillations from 0 to
, and the function makes two complete oscillations from 0 to

You can see the two functions in the image below. You can also see that the two graphs cross 4 times, meaning that the equation
 has four solutions.
has four solutions.