Question

rooks are randomly placed on different squares of a chessboard. A rook is said to attack all of the squares in its row and its column. Compute the probability that every square is occupied or attacked by at least rook. You may leave unevaluated binomial coefficients in your answer.

Answer 1

This probabilistic question involves calculating the chance that all squares of a chessboard are occupied or attacked by rooks. The answer requires complex combinatorial calculations. Insufficient detail is provided to compute a definitive solution.

Step-by-step explanation:

The question asks for the calculation of the probability that all squares on a chessboard are occupied or attacked by at least one rook if rooks are placed randomly on the chessboard. To calculate this, one would need to use principles of combinatorics and probability theory. However, with the information provided, we do not have sufficient detail to provide a step-by-step answer. The probability that each square is either occupied or attacked depends on the number of rooks placed and their positions, and requires a complex calculation involving different scenarios and combinatorial counting.

Answer 2

Answer:
`2*8^(8)-8!`

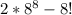
Step-by-step explanation:

We can place a rook in each row in
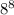`8^(8)` ways.

We can place a rook in each column in
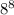`8^(8)` ways.

So the total ways in which we can place a rook in a row or column is
`2*8^(8)`

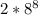
Now there are 8 ways to choose the column for the first row, 7 ways to choose the column for the second row, and so on. So there are 8! ways to choose a column for a row.

So, we get the final answer by subtracting the 8! from the total ways a rook can be placed which is
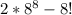`2*8^(8)-8!` when binomial coefficients are not evaluated