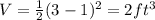Answer:
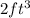
Explanation:
We are given that
Side of square shaped piece= 3ft
Let square of side x cut from each corner of square piece cardboard.
Length of box=

Breadth of box=

Height of box= x
We have to find the largest volume of box.
Volume of box is given by
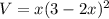
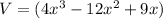
Differentiate w.r.t x
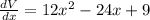
Substitute
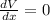

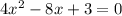
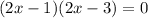
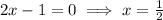
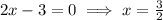

Again differentiate w.r.t x
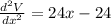
Substitute
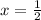
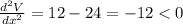
Substitute
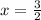
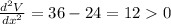
Therefore,
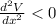 at
at
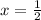
Hence, the volume is maximum at
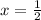
Substitute the value
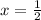 then we get
then we get