Question

You have 100 cm of string which can be cut in one place (or not cut at all) and then formed into a circle and a square (or just a square or just a circle). Where should you cut the string to get the maximum area? The minimum area?

Answer 1

44cm for minimum area and 0 for maximum area (circle)

Explanation:

Let's C be the circumference of the circle and S be the circumference of the square. If we cut the string into 2 pieces the total circumferences would be the string length 100cm.

S + C = 100 or S = 100 - C

The side of square is S/4 and radius of the circle is
`(C)/(2\pi)`

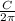
So the area of the square is

`A_S = (S^2)/(4^2) = (S^2)/(16)`

`A_C = \pi(C^2)/((2\pi)^2) = (C^2)/(4\pi)`

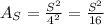
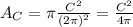
Therefore the total area is

`A = A_S + A_C = (S^2)/(16) + (C^2)/(4\pi)`

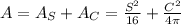
We can substitute 100 - C for S

`A = ((100 - C)^2)/(16) + (C^2)/(4\pi)`

`A = (100^2 - 200C + C^2)/(16) + (C^2)/(4\pi)`

`A = 625 -12.5C + (C^2)/(16) + (C^2)/(4\pi)`

`A = 625 -12.5C + C^2((1)/(16) + (1)/(4\pi))`

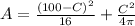
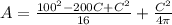
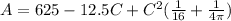
To find the maximum and minimum of this, we can take the first derivative and set that to 0

`A^(') = -12.5 + 2C((1)/(16) + (1)/(4\pi)) = 0`

`C((1)/(8) + (1)/(2\pi)) = 12.5`

`C \approx 44 cm`

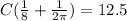
If we take the 2nd derivative:

`A^('') = (1)/(8) + (1)/(2\pi) > 0`

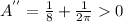
We can see that this is positive, so our cut at 44 cm would yield the minimum area.

The maximum area would be where you not cut anything and use the total string length to use for either square or circle

if C = 100 then
`A_C = (C^2)/(4\pi) = (100^2)/(4\pi) = 795.77 cm^2`

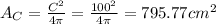
if S = 100 then
`A_S = (S^2)/(16) = (100^2)/(16) = 625 cm^2`

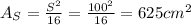
So to yield maximum area, you should not cut at all and use the whole string to form a circle