Question

A bullet of mass 6.00 g is fired horizontally into a wooden block of mass 1.12 kg resting on a horizontal surface. The coefficient of kinetic friction between block and surface is 0.250. The bullet remains embedded in the block, which is observed to slide a distance 0.300 m along the surface before stopping. What is the initial speed of the bullet?

Answer 1

vo = 227 m/s

Step-by-step explanation:

Let's analyze the problem, we have two parts one during the crash for which we will use the moment and another when it slides where we will use the energy. As we give the data of the latter let's start here

Before starting let's reduce the unit to the SI system

m = 6.00 g (1kg / 1000g) = 6.00 10⁻³ kg

M = 1.12 kg

We write the energy at two points, one initial right after the crash and another when the body has stopped

Just after shock

The bodies are united, so the mass is the sum of the mass of the bullet and the block

Em₀ = K = ½ (m + M) v²

When the body has stopped

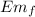`Em_(f)` = 0

When in the system there is friction force the variation the mechanical energy is equal to the work of the friction force. Notice that the force of friction opposes the movement so that their work is negative

W fr = ΔEm =
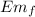`Em_(f)` -Em₀

-fr d = 0 - ½ (m + M) v²

To find the force of friction let's use Newton's second law

Axis y

N-W = 0

N = W = (m + M) g

The equation for the force of friction is

fr = μ N

fr = μ (m + M) g

Let's replace in the work and energy equation

-μ (m + M) g d = 0 - ½ (m + M) v²

From here we can find the system speed. Let's calculate

v³ = 2 μ g d

v = √ (2μ gd)

v = √ (2 0.250 9.8 0.300)

v = 1.21 m / s

Now let's solve the crash, let's look for the moment before and after it

Before the crash

po = m vo

After the crash

`p_(f)` = (m + M) v

The system is formed by the bullet and the block, therefore, the forces during the impact are internal and the amount of movement is conserved

po =
`p_(f)`

m vo = (m + M) v

vo = v (m + M) / m

vo = 1.21 (0.00600 + 1.12) /0.00600

vo = 227 m / s