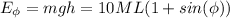Answer:
(a) 0
(b) 10ML
(c)
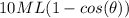
(d)
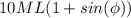
Step-by-step explanation:
(a) When hanging straight down. The child is at the lowest position. His potential energy with respect to this point would also be 0.
(b) Since the rope has length L m. When the rope is horizontal, he is at L (m) high with respect to the lowest swinging position. His potential energy with respect to this point should be
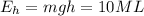
where g = 10m/s2 is the gravitational acceleration.
(c) At angle
 from the vertical. Vertically speaking, the child should be at a distance of
from the vertical. Vertically speaking, the child should be at a distance of
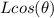 to the swinging point, and a vertical distance of
to the swinging point, and a vertical distance of
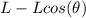 to the lowest position. His potential energy to this point would be:
to the lowest position. His potential energy to this point would be:
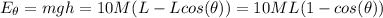
(d) at angle
 from the horizontal. Suppose he is higher than the horizontal line. This would mean he's at a vertical distance of
from the horizontal. Suppose he is higher than the horizontal line. This would mean he's at a vertical distance of
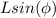 from the swinging point and higher than it. Therefore his vertical distance to the lowest point is
from the swinging point and higher than it. Therefore his vertical distance to the lowest point is
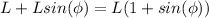
His potential energy to his point would be: